In spite of our best efforts we could not find a fixed point with respect to which we should study absolute rest and absolute motion. So, the study of relative rest and relative motion assumes importance.
Consider two cars A and B running parallel to each other on same road with same velocities. No doubt the speedo meter of each indicates motion but the two drivers will always find themselves facing each other.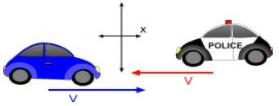
Relative velocity of a body A with respect to another body B, when both are in motion, is the velocity with which A appears to move B.
Relative Velocity Formula: Relative velocity is used to describe the motion of airplanes in the wind or moving boats through water etc. This velocity is computed according to the observer inside the object. This can be computed by introducing an intermediate frame of references. In simple words, this can be the vector some of the velocities. Formula for relative velocity is articulated ad,
\(\overrightarrow{{{V}_{AC}}}\,=\,\overrightarrow{{{V}_{AB}}}\,+\,\overrightarrow{{{V}_{BC}}}\)
Where, VAB is the velocity with respect to A and B. VBC is the velocity with respect to B and C. VAC is the velocity with respect to A and C.
Physics Significance: Let two cars move in a single direction. Two persons A and B are sitting in the vehicles shown. Assume the velocities are VA = 6 m/s and VB = 4 m/s. The person A notices person B to be moving towards him with a speed of (6 – 4) m/s = 2 m/sec. That is the velocity of B with respect to A. That means \(\overrightarrow{{{V}_{BA}}}\) is directed from B to A.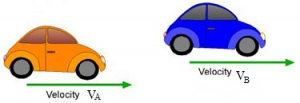
Now, A seems to move towards B with a speed of 4 m/sec. That means the velocity of A relative to B \((\overrightarrow{{{V}_{AB}}})\) has the magnitude 4 m/sec and directed from A to B.
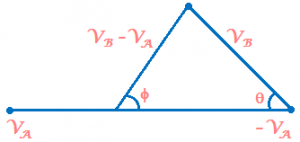Therefore,
\(\overrightarrow{{{V}_{AB}}}=-\overrightarrow{{{V}_{BA}}}\)
\(\overrightarrow{{{V}_{BA}}}=\overrightarrow{{{V}_{B}}}-\overrightarrow{{{V}_{A}}}\)
So,
\(|\overrightarrow{{{V}_{BA}}}|\,=\,|\overrightarrow{{{V}_{AB}}}|\)
\({{V}_{AB}}\,=\,\sqrt{{{V}_{A}}^{2}+{{V}_{B}}^{2}-2{{V}_{A}}{{V}_{B}}\cos \theta }\)
\(\theta ={{\tan }^{-1}}\left( \frac{{{V}_{B}}\sin \theta }{{{V}_{A}}-{{V}_{B}}\cos \theta } \right)\)
Real life Examples:
- If you have ever been in a car stopped at red light and felt like your car was creeping forward, you have experienced relative motion. If your car is not moving at all, but you sense motion, it’s probably because the car next to you is creeping forward. But it feels like, seems like you are creeping forward.
- Imagine you are in a speeding car. You have a small ball like a tennis ball. You toss it up, and it falls back straight down into your hand.
If a person outside the car standing by the road was watching this, they would see the ball go up and down, but while it was doing that, it would be moving as fast as the car down the road. If that same person threw a ball along the road, its motion would look similar to them.
To you, though, the ball just goes straight up, and straight down Relative to You.
Relative to the observer by the road, the ball basically just moves in a straight line down the road with only a tiny part of that motion being up and down.
So, the ball has quite different relative motions from the perspectives of the car passenger and the person standing by the road.
Problem: A train travels with a speed of 70m/s with regards to the ground in the east direction. A spectator is moving with a speed of -15m/s with regards to the train in west direction. Compute the speed of man with respect to the ground?
Solution: Given,
VBC = Velocity of train with respect to ground = 70m/sec
VAB = Velocity of man with respect to train = – 15 m/sec
VAC = Velocity of man with respect to ground =?
Now,
\(\overrightarrow{{{V}_{AC}}}=\overrightarrow{{{V}_{AB}}}+\overrightarrow{{{V}_{BC}}}\)
\(\overrightarrow{{{V}_{AC}}}\) = -15 + 70 = 55 m/sec.