Pairs of tangents: From a given point two tangents can be drawn to a circle which are real and distinct, coincident or imaginary according as the given point lies outside on or inside the circle.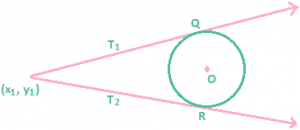
The combined equation of the pair of tangents drawn from point P(x₁, y₁) to the circle x² + y² = a² is (x² + y² – a²) (x₁² + y₁² – a²) = (xx₁² + yy₁² – a²)².
⇒ SS₁ = T² where T = xx₁ + yy₁ – a².
Length of the tangents:
- The length of the tangent from the point P(x₁, y₁) to the circle x² + y² + 2gx + 2fy + c = 0, length of the tangent (√S₁) = √( x₁² + y₁² + 2gx₁ + 2fy₁ + c).
- If PT is the length of the tangent from a point P to a given circle, then PT² is called the power of the point with respect to the given circle.
- If we write S = x² + y² + 2gx + 2fy + c and S₁ = x₁² + y₁² + 2gx₁ + 2fy₁ + c, then equation of circle is S = 0 and length of tangent is √S₁ from P(x₁, y₁) the power of point P(x₁, y₁) is S₁.
Example: Find the length of the tangents drawn from the point (3, -4) to the circle 2x² + 2y² – 7x – 9y – 13 = 0.
Solution: The equation of the given circle is 2x² + 2y² – 7x – 9y – 13 = 0.
\({{x}^{2}}+{{y}^{2}}-\frac{7}{2}x-\frac{9}{2}y-\frac{13}{2}=0\).
Here, \(S={{x}^{2}}+{{y}^{2}}-\frac{7}{2}x-\frac{9}{2}y-\frac{13}{2}\).
\({{S}_{1}}={{3}^{2}}+{{\left( -4 \right)}^{2}}-\frac{7}{2}\times 3-\frac{9}{2}\times \left( -4 \right)-\frac{13}{2}\).
\(=9+16-\frac{21}{2}+18-\frac{13}{2}=26\).
Hence, required length of the tangent = √S₁ = √26.
Director circle: The locus of the point of intersection of two perpendicular tangents to a given conic is known as its director circle. The equation of director circle of circle x² + y² = a² is x² + y² = 2a².