Continuous Meaning: We say a function f (x) is continuous at a point x = a it means at a point (a, f (a)). The graph of the function has no holes or graphs. That is, its graph is unbroken at point (a, f (a)).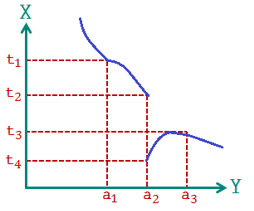
The continuity at x = a2 if \(\underset{x\to {{a}_{2}}}{\mathop{\lim }}\,f\left( x \right)\). does not exist.
Continuity at a point: A function f (x) is said to be continuous at a point x = a of its domain if \(\underset{x\to a}{\mathop{\lim }}\,f\left( x \right)=f\left( a \right)\).
Thus, (f (x) is continuous at x = a).
⇒ \(\underset{x\to a}{\mathop{\lim }}\,f\left( x \right)=f\left( a \right)\).
⇒ \(\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f\left( x \right)=f\left( a \right)\).
If f (x) is not continuous at a point x = a, then it is said to be discontinuous at x = a.
If \(\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f\left( x \right)\ne f\left( a \right)\), then the discontinuity is known as the removable discontinuity because f(x) can be made continuous by re-defining it at point x = a in such a way that \(f\left( a \right)=\underset{x\to a}{\mathop{\lim }}\,f\left( x \right)\).
If \(\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f\left( x \right)\ne \underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f\left( x \right)\), then f (x) is said to have a discontinuity of first kind.
A function f (x) is said to have a discontinuity of the second kind at x = a if \(\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f\left( x \right)\) or \(\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f\left( x \right)\) or both do not exist.
Continuity on an open interval: A function f (x) is said to be continuous on an open interval (a, b) if it is continuous at every point on the interval (a, b).
Continuity on a closed interval: A function f (x) is said to be continuous on a closed interval {a, b} if
1. f is continuous on the open interval (a, b)
2. \(\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f\left( x \right)=f\left( a \right)\).
and,
3. \(\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f\left( x \right)=f\left( b \right)\).
In order words, f (x) is continuous on [a, b] if it is continuous on (a, b) and it is continuous at a form the right and at b form the left.