A plane is a surface such that if any two points are taken on it, the line segment joining them lies completely on the surface. In other words, every point on the line segment joining any two points lies on the plane.
Every first degree equation x, y and z represents a plane i.e., ax +by + cz + d = 0 is the general equation of a plane.
Equations of a Plane passing through given Point: The general equation of a plane passing through a point (x1, y1, z1) is
a (x – x1) + b (y – y1) + c (z – z1) =0.
Three Point Form of a Plane: Let ax + by + cz + d = 0 … (i)
Be the equation of a plane passing through three points P (x1, y1, z1), Q (x2, y2, z2), R (x3, y3, z3)
⇒ \(\left| \begin{matrix}x & y & z & 1 \\{{x}_{1}} & {{y}_{1}} & {{z}_{1}} & 1 \\{{x}_{2}} & {{y}_{2}} & {{z}_{2}} & 1 \\{{x}_{3}} & {{y}_{3}} & {{z}_{3}} & 1 \\\end{matrix} \right|=0\).
If four points P (x1, y1, z1), Q (x2, y2, z2), R (x3, y3, z3) and S (x4, y4, z4) are coplanar, then the plane through three points also passes through fourth point.
Thus, the condition of co-planarity of four points is
⇒ \(\left| \begin{matrix}x & y & z & 1 \\{{x}_{1}} & {{y}_{1}} & {{z}_{1}} & 1 \\{{x}_{2}} & {{y}_{2}} & {{z}_{2}} & 1 \\{{x}_{3}} & {{y}_{3}} & {{z}_{3}} & 1 \\\end{matrix} \right|=0\).
Intercept Form of a Plane: The equation of a plane intercepting lengths a, b and c with x – axis, y – axis and z – axis respectively is \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\).
To determine the intercepts made by a plane with the coordinate axes we proceed as follows:
For x – intercept: put y = 0, z = 0 in the equation of the plane and obtain the value of x. The value of x is the intercept on x – axis.
For y – intercept: put x = 0, z = 0 in the equation of the plane and obtain the value of y. The value of y is the intercept on y – axis.
For z – intercept: put x = 0, y = 0 in the equations of the plane and obtain the value of z. The value of z is the intercept on z – axis.
Normal Form of a Plane: The equation of a plane at a distance p form the origin and having direction cosines l, m, n of a normal to it is lx + my + nz = p.
Equation of a Parallel Plane: The equation of a plane parallel to the plane ax + by + cz + k = 0.
Equation of Planes Bisecting the Angle between Two Given Planes: The equation of the planes bisecting the angles between the planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0.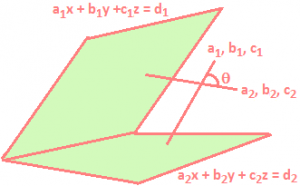
Are given by \(\frac{\left( {{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}z+{{d}_{1}} \right)}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}}=\pm \frac{\left( {{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}z+{{d}_{2}} \right)}{\sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\).
Equation of a Plane Passing through the Intersection of two Planes: The equation of a plane passing through the intersection of a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 is (a₁x + b₁y + c₁z + d₁) + λ (a₂x + b₂y + c₂z + d₂) = 0, where λ is a constant.
Example: Find the equation of the plane containing the line of intersection of the plane x + y + z – 6 = 0 and 2x + 3y + 4y + 5 and passing through the point (1, 1, 1).
Solution: The equation of the plane through the line of intersection of the given planes is
(x + y + z – 6) + λ (2x + 3y + 4y + 5) = 0 … (i)
If (i) passes through (1, 1, 1), then
– 3 + 14 λ = 0 ⇒ λ = 3/14.
Putting λ = 3/14 in (i), we obtain the equation o the required plane as
(x + y + z – 6) + λ = 3/14 (2x – 3y + 4y + 5) = 0
20x + 23y + 26z – 69 = 0.
