A particle executing SHM possesses two types of energy if a particle executes SHM, its kinetic energy changes into potential energy and vice-versa keeping total energy constant (if friction of air is neglected).
Kinetic energy: This is an account of the velocity of the particle.
K = ½ mv2
= ½ mA2 ω2cos2 (ωt + φ) = ½ m ω2 (A2 –X2)
From this expression, we conclude that kinetic energy is maximum at the centre(x = ±A).
Potential energy: This is an account of the displacement of the particle from its mean position.
U = ½ m ω2x2 = ½ mA2 ω2sin2 (ωt + φ)
Thus, potential energy has its minimum at the centre (x = 0) and increases as the particle approaches either extreme of oscillation (x = ±A).
Thus, total energy = kinetic energy + potential energy
Or E = ½ m ω2A2
Obviously, the total energy is constant and is proportional to the square of amplitude (A) of motion. Figures show the variations of total energy (E), potential energy (U) and kinetic energy (K) with displacement(x).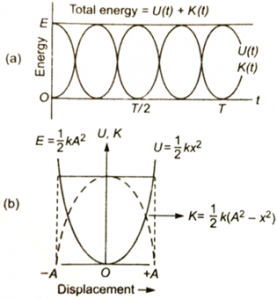
Example: A body is executing simple harmonic motion at a displacement x its potential energy is E1 and at a displacement y it potential energy is E2. The potential energy (E) at displacement (x + y) is
Solution: Potential energy of a body executing SHM
U = ½ m ω2y2
∴ U1 = ½ mω2y2
\(x=\sqrt{\frac{2{{U}_{1}}}{m{{\omega }^{2}}}}\)And U2 = ½ mω2y2
\(y=\sqrt{\frac{2{{U}_{2}}}{m{{\omega }^{2}}}}\)At displacement (x + y)
U = ½ mω2(x + y) 2
\(\left( x+y \right)=\sqrt{\frac{2U}{m{{\omega }^{2}}}}\) \(\sqrt{\frac{2{{U}_{1}}}{m{{\omega }^{2}}}}+\,\sqrt{\frac{2{{U}_{2}}}{m{{\omega }^{2}}}}=\,\sqrt{\frac{2U}{m{{\omega }^{2}}}}\)∴ √U1 + √U2 = √U
i.e., √E = √E1 + √E2