Theorem of Parallel Axes: This theorem states that the moment of inertia I of a body about any axis is equal to its moment of inertia about a parallel axis through its centre of mass, plus the product of the mass M of the body and the square of the perpendicular distance a between the two axes. That is
I = Icm + Ma².
Proof: Let C be the centre of mass of a plane lamina. Let I be its moment of inertia about an axis AB in its plane and Icm the moment of inertia about a parallel axis EF passing through C. Let the distance between EF and AB be a.
Let us consider a particle P of mass m at a distance r from EF. Its distance from AB is (r + a), and its moment of inertia about it is m (r + a)². Therefore the moment of inertia of the lamina about AB is given by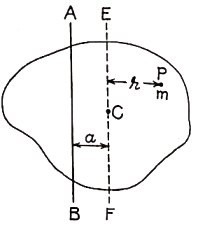 I = ∑ m (r + a)² = ∑m (r² + a² + 2ar)
I = ∑ m (r + a)² = ∑m (r² + a² + 2ar)
I = ∑mr² + a² ∑m + ∑2mar
Since a is constant, it can be taken outside ∑
.˙. I = ∑mr² + a² ∑m + 2a∑mr.
Now, ∑mr² = Icm, where Icm is the moment of inertia of the lamina about EF; a² ∑m = a² ∑M, where M is the total mass of the lamina, and ∑mr = 0 because the sum of the moments of all the mass particles of a body about an axis through the centre of mass of the body is zero. Hence, making these substitutions in we get
I = Icm + Ma²
Theorem of Perpendicular Axes: This theorem states that the moment of inertia of a uniform plane lamina about an axis perpendicular to its plane is equal to the sum of its moments of inertia about any two mutually perpendicular axes in its plane intersecting on the first axis.
Proof: Let OZ be the axis perpendicular to the plane of the lamina about which the moment of inertia is to be taken. Let OX and OY be two mutually perpendicular axes in the plane of the lamina and intersecting on OZ. Let us consider a particle P of mass m at distance r from OZ. The moment of inertia of this particle about OZ is m r². Therefore the moment of inertia Iz of the whole lamina about OZ is Iz = ∑ m r².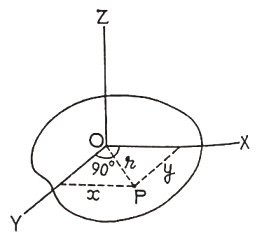 But r² = x² + y², where x and y are the distance of P from OY and OX respectively.
But r² = x² + y², where x and y are the distance of P from OY and OX respectively.
.˙. Iz = ∑ m(x² + y²) = ∑mx² + ∑my².
But ∑mx² is the moment of inertia Iy of the lamina about OY, and ∑my² is the moment of inertia Ix of the lamina about OX.
.˙. Iz = Iy + Ix
