Moment of a force (or torque) is a physical quantity which tries to rotate or rotate a body about a given point or a given axis of rotation. Or the turning effect of a force acting on a body about an axis is called the moment of force or torque.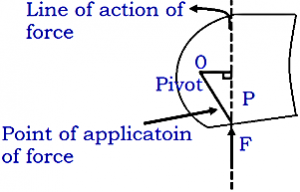 Factors affecting the turning of a body:
Factors affecting the turning of a body:
The magnitude of the force applied and
The distance of line of action of the force from the axis of rotation.
Definition of moment of a force (or torque):
The moment of a force (or torque) is equal to the product of the magnitude of the force and the perpendicular distance of the line of action of the force from the axis of rotation.
Moment of force can be calculated by two methods: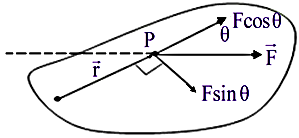 By taking components of force F
By taking components of force F
τ [Tau]
τ = r * (F sin θ)
τ = r * F sin θ
By taking components of vector
τ = (r sin θ) F
τ = F r sin θ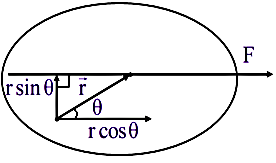 ANGULAR MOMENTUM AND ITS CONSERVATION:
ANGULAR MOMENTUM AND ITS CONSERVATION:
Angular momentum of a rigid body undergoing pure rotation about a fixed axis is given by
\(\overrightarrow{L~}=I~\vec{\omega }\)Where I is the moment of inertia of the body about the axis of rotation and ω its angular velocity. It is related to torque much like linear momentum is related to force:
\(\overrightarrow{~F}=\frac{d\vec{p}}{dt}\) \(\overrightarrow{~\tau }=\frac{d\vec{L}}{dt}\)Angular momentum is a vector quantity and it is directed along, provided I can be treated as a scalar (i.e. the rotation is along one of the axes of symmetry).
Angular momentum is conserved if the net torque acting on a body about the given axis is zero. The law of conservation of angular momentum is frequently used, for example in analyzing motion under a central force, collisions between extended bodies, etc.
