ocal chord: A chord of parabola is a focal chord, if it passes through focus
Some other standard forms of parabola:
A. y² = – 4ax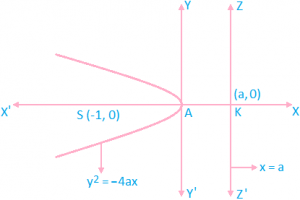
- Co – ordinates of vertex = (a, 0)
- Co – ordinates of focus = (-a, 0)
- Equation of directrix = x – a = 0
- Equation of axis is y = 0
- Length of latus rectum = 4a
- Focal distance = a – x
B. x² = 4ay
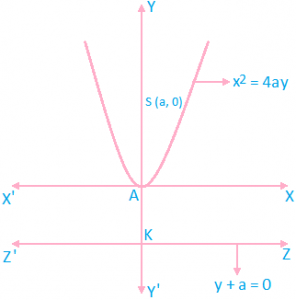
- Co – ordinates of vertex = (0, 0)
- Co – ordinates of focus = (0, a)
- Equation of directrix is y + a = 0
- Equation of axis is x = 0
- Length of latus rectum = 4a
- Length of focal distance to point P(x, y) = (a + y)
C. x² = – 4ay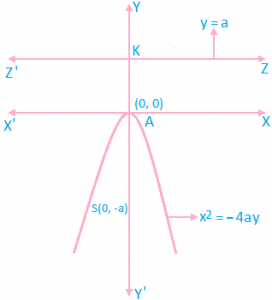
- Co – ordinates of vertex = (0, 0)
- Co – ordinate of focus = (0, -a)
- Equation of directrix is y – a = 0
- Equation of axis is x = 0
- Length of latus rectum = 4a
- Focal distance at a point P(x, y) = a – y
Here is a table which are all together
|
y² = 4ax |
y² = – 4ax | x² = 4ay |
x² = – 4ay |
||
|
1 |
Co – ordinates of vertex | (0, 0) | (0, 0) | (0, 0) |
(0, 0) |
|
2 |
Co – ordinates of focus | (a, 0) | (-a, 0) | (0, a) |
(0, -a) |
|
3 |
Equation of directrix | X = – a | X = a | Y = -a |
Y = a |
|
4 |
Equation of axis | Y = 0 | Y = 0 | X = 0 |
X = 0 |
|
5 |
Length of latus rectum | 4a | 4a | 4a |
4a |
|
6 |
Focal distance of a point P(x, y) | a + x | a – x | a + y |
a – y |
If vertex of a parabola at a point A (h, k) and its latus – rectum of length 4a then its equation is
- (y – K)² = 4a (x – h), if it axis is parallel to OX that is parabola open right ward.
- (y – K)² = – 4a (x – h), if its axis is parallel to OX’, that is opens leftward.
- (x – h)² = 4a (y – k), if its axis is parallel to OY that is opens upward.
- (x – h)² = – 4a (y – k), if its axis is parallel to OY’ that is opens downward.
Parametric equation of parabola: co – ordinates of any point on parabola y² = 4ax is (at², 2at) where t ϵ R.
The equation x = at², y = 2at taken together are called the parametric equation of parabola.
The parametric equation of (y – k)² = 4a (x – h) are x = h + at², y = k + 2at.
|
parabola |
y² = 4ax | y² = – 4ax | x² = 4ay |
x² = – 4ay |
|
Parametric co -ordinates |
(at², 2at) | (-at², 2at) | (2at, at²) |
(2at, – at²) |
|
Parametric equation |
x = at², y = 2at | x = – at², y = 2at | x = 2at, y = at² |
x = 2at, y = -at² |
If suppose the equation of parabola is quadratic in both x and y, then to find its vertex focus, axis
First obtain the equation of parabola and express it in here form (ax + by + c)² = [Constant] (bc – ay + c’). If should be noted here that ax + by + c & bx + ay + c are perpendicular lines.
Divide both sides by √ (a² + b²) to obtain
\({{\left( \frac{ax+by+x}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right)}^{2}}=\left( constant \right)\left( \frac{bx-ay+c’}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right)\)Put \(\frac{ax+by+x}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\) = Y and \(\frac{bx-ay+c’}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\)= X
We get
y² = (constant) X
Compare y² = 4ax to obtain vertex, focus, axis etc.
