- Discovered by Andrews for CO2
- Above a certain temperature, it is impossible to liquefy a gas.
- The temperature below which a gas can be compressed by applying only pressure is called critical temperature (Tc).
- The pressure applied to liquefy gas is called critical pressure Pc
- The volume occupied by one mole of the substance is called critical volume Vc
- The pressure v/s volume plot for CO2 is
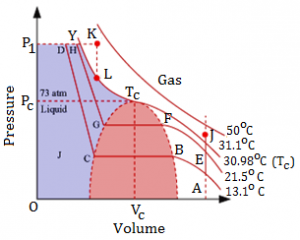
- At low temperature, say 13.1˚C, the CO2 is entirely gaseous.
- As pressure is increased, the volume decreases from A to B.
- At B, deviations from Boyle’s law (P V) start. The volume decreases rapidly till C. between B & C, CO2 exists both as a liquid and gas and pressure remains constant.
- After C, CO2 is completely liquefied and on increasing pressure further only slight decrease in volume is seen.
- The pressure corresponding to the horizontal line BC is the vapour pressure of liquid.
- As the temperature is raised, the horizontal portion becomes smaller till 31.1˚C where it reduces to a point Tc. At Tc the boundary between liquid and gas disappears.
- Above 31.1˚C, no liquefaction is seen.
- Thus, it can be seen that liquefaction of gases is possible only at lower temperatures.
Van der Waal’s Equation and the Critical Point:
The constant of Van der Waal’s equation can be obtained from the critical point data.
The Van der Waal’s Equation can be arranged as follow:
P = RT / (V – b) – a / V2
To investigate the horizontal point of inflection on a plot of P versus V, we obtain
dP/dV = -RT/ (V – b2) + 2a / V3
d2P/ dV = 2RT/ (V – b)3 – 6a/V4
At gas-liquid equilibrium, i.e. at critical-point,
P = Pc
V = Vc
T = Tc
And first order and second order derivative of P with respect to V are zero.
Therefore we can write;
Pc = RTc /(Vc – b) – a / Vc3
0 = RTc /(Vc – b2) + 2a / Vc3
0 = 2RTc / (Vc – b)3 – 6a / Vc4
These equations can be solved to get
a = 3PcV2c
b = Vc/3
R = 8 PcVc/ 3Tc
(PcVc) / (RTc) = 8/3 = 0.375
Thus,
Zc = 0.375, which is a compressibility factor at critical point.
Since R is a gas constant, and the values of a and b are different for different gases.
They can be calculated in terms of critical-point quantities Pc and Tc by substituting
Vc = 3 RTc / (8Pc)
a = 27R2T2c / (64Pc)
b = RTc / (8 Pc)
