Enthalpy or Heat of Combustion:
It is the amount of heat evolved or decreased in enthalpy when one mole of a substance is completely oxidized.
Organic compounds containing only carbon, hydrogen, and oxygen are burnt to gaseous carbon dioxide and liquid water.
For example,
C2H6(g) + 3.5O2(g) → 2CO2(g) + 3H2O(l); ΔH = − 372.8 kcal
Enthalpy or Heat of Solution:
The amount of heat evolved or absorbed when one mole of solute is dissolved in excess of solvent so that further addition of solvent makes no heat change.
For example,
NH4Cl(s) + H2O(l) → NH4Cl(aq); ΔH = + 3.90 kcal
If an ionic compound is dissolved in water, the enthalpy of solution is determined by the selective values of the lattice enthalpy, Δlattice H⊝ and enthalpy of hydration of ions, ΔHyd H⊝ as
Δsol H⊝ = Δlattice H⊝ + ΔHyd H⊝
For most of the ionic compounds, Δ sol H⊝ is positive and the dissociation process is endothermic. Therefore the solubility of most salts in water increases with rise of temperature.
If the lattice enthalpy is very high, the dissolution of the compound may not take place at all.
Lattice Enthalpy:
The lattice enthalpy of an ionic compound can be described in 2 ways:
- It is the enthalpy change which occurs when one mole of an ionic compound dissociates into its ions in gaseous state. Lattice dissociation enthalpies are always positive.
- It is the enthalpy change when 1 mole of an ionic compound is formed from its scattered gaseous ions. Lattice formation enthalpies are always negative.
Calculating lattice enthalpy:
It is impossible to measure the enthalpy change starting from a solid crystal and converting it into its scattered gaseous ions. It is even more difficult to imagine how you could do the reverse – start with scattered gaseous ions and measure the enthalpy change when these convert to a solid crystal. We can use a Hess’s Law cycle (in this case called a Born-Haber cycle) involving enthalpy changes which can be measured. Lattice enthalpies calculated in this way are described as experimental values.
Born-Haber cycles:
Born-Haber cycle for sodium chloride
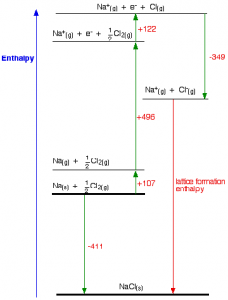
Notice that we only need half a mole of chlorine gas in order to end up with 1 mole of NaCl. The Born-Haber cycle now imagines this formation of sodium chloride as happening in a whole set of small changes, most of which we know the enthalpy changes for – except, of course, for the lattice enthalpy that we want to calculate.
- The +107 kJ/mol is the atomisation enthalpy of sodium. We have to produce gaseous atoms so that we can use the next stage in the cycle.
- The +496 kJ/mol is the first ionisation energy of sodium to convert gaseous atoms to gaseous singly charged positive ions.
- The +122 kJ/mol is the atomisation enthalpy of chlorine. Again, we have to produce gaseous atoms so that we can use the next stage in the cycle.
- The -349 kJ/mol is the first electron affinity of chlorine to convert gaseous atoms to gaseous singly charged negative ions.
- And finally, we have the positive and negative gaseous ions that we can convert into the solid sodium chloride using the lattice formation enthalpy.
Now we can use Hess’s Law to find lattice enthalpy
-411 = + 107 + 496 + 122 – 349 + LE
LE = + 411 + 107 + 496 + 122 – 349
LE = + 787 kJ mol-1
Heat of Dilution:
The amount of heat evolved or absorbed when solution containing one mole of solute is diluted from one concentration to another.
For example, diluting an acid with water to prepare a solution with lesser acid concentration.
Enthalpy or Heat of Neutralization:
The amount of heat evolved when one gram equivalent of an acid is completely neutralized by one gram equivalent of a base in dilute solution is called heat of neutralization.
For example,
HCl(aq) + NaOH(aq) → NaCl(aq) + H2O; ΔH = − 13.7 kcal
Heat of atomization:
The amount of heat required for the formation of one mole of atoms in gaseous state from its elements is known as heat of atomization of that element.
C(s) → C(g); ΔH = 171.7 kcal/mol
H2(g) → 2H(g); ΔH = 104 kcal
Bond Energies/Enthalpies:
- The amount of energy required to break one mole of a particular type of bond between the atoms in the gaseous state.
- Energy required to separate the atoms in the gaseous state under 1 atm pressure and the specified temperature is called bond dissociation energy.For example.
H − H(g) → 2H(g); ΔH = 433 kJ/mol
H − I(g) → H(g) + I(g); ΔH = 299 kJ/mol - The bond dissociation energy of a diatomic molecule is also called bond energy.
- The bond dissociation energy depends on the nature of bonds and also on the molecule in which the bond is present.
- When a molecule of a compound contains more than one bond of the same kind, the average value of the dissociation energies of a given bond is taken.
- This average bond dissociation energy required to break each bond in a compound is called the bond energy which is also the heat of formation of the bond from gaseous atoms constituting the bond with reverse sign.
- Consider the dissociation of water molecule,
H2O(g) → H(g) + O − H(g); ΔH = 497.8 kJ/mol - The average of these two bond dissociation energies gives the value of bond energy of O-H bond
- Therefore, Bond energy of O – H bond = 497.8 + 428.52 = 463.15 kJ/molBond energies can be obtained from the data of heats of combustion and heats of dissociation.
O − H(g) → H(g) + O(g); ΔH = 428.5 kJ/mol
Application of bond energies:
a. Determination of heat of reactions:
ΔrH = Sum of bond energies of reactants – Sum of bond energies of products
b. Determination of resonance energy:
Resonance energy = Experimental actual heat of formation – Calculated heat of formation
