Radical axis: The radical axis of two circles is the locus of a point which moves in such a way that length of the tangent drawn from it to the two circles are equal.
The radical axis of circles S₁ = 0 and S₂ = 0 is given by S₁ – S₂ = 0.
Properties of radical axis:
i) The equations of radical axis and common chord are equal. They are equal but geometrically, we have following distinctions.
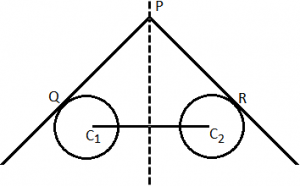
- C₁C₂ > r₁ + r₂.
In this case, radical axis exist but common chord does not exist.
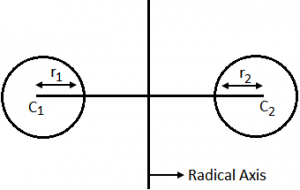
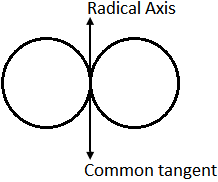
- Two circles touch externally to each other C₁C₂ = r₁ + r₂.
In this case both exist but length of common chord is zero i.e., it is a common tangent.
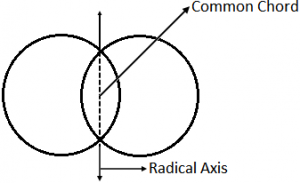
- Circles intersect: r₁ – r₂ < C₁ + C₂ < r₁ + r₂.
In this case radical axis and common chord exist but points lying on common chord do not lie on the radical axis.
- When one circle lies inside the other C₁C₂ < r₁ – r₂.
In this case, the radical axis and common chord both does not exist.
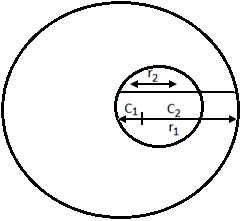
ii) Radical axis is always perpendicular to the line joining the centres of the circle.
iii) The radical axis of three circle whose centres are non-collinear, taken in pairs are concurrent.
iv) The centre of the circle cutting two given circles orthogonally lies on their radical axis.
