Kirchhoff’s Voltage Law:
Kirchhoff’s voltage law states that the algebraic sum of all branch voltages around any closed loop of a network is zero at all instants of time. It is a consequence of the law of conservation of energy. Voltage being the energy (or work) per unit charge.
A simple resistive network with voltage reference directions assigned for the elements and a clockwise loop direction selected for the application of the KVL. Starting at node A, we assign a positive sign to the voltage if the polarity marks occur in the order + to -, a negative sign for the opposite order. Thus we write
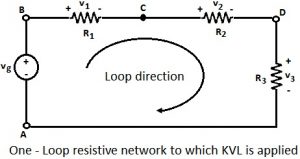
– Vg + V₁ + V₂ + V₃ = 0
KVL can be written as ∑Closed path V = 0
Kirchhoff’s Current Law:
Kirchhoff’s Current Law states that the algebraic sum of branch currents at a node is zero at all instants of the time. The law is a consequence of conservation of charge. Charge which enters a node must leave that node because it cannot be stored there. Since the algebraic summation of charge must be zero, the time derivative of this summation must also equal to zero. Therefore, KCL can be stated as:
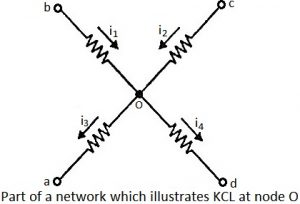
i₁ + i₂ – (i₃ + i₄) = 0
Or i₁ + i₂ = i₃ + i₄
KCL can be written as ∑node ‘n’ i = 0
