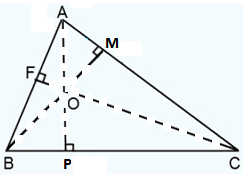
Orthocenter of a Triangle

The orthocenter of a triangle is the point of intersection of altitudes. The coordinates of orthocenter of a triangle whose vertices are A (x₁, y₁), B (x₂, y₂) and C (x₃, y₃) are given as O

\(\left( \frac{{{x}_{1}}\tan A+{{x}_{2}}\tan B+{{x}_{3}}\tan C}{\tan A+\tan B+\tan C},\frac{{{y}_{1}}\tan A+{{y}_{2}}\tan B+{{y}_{3}}\tan C}{\tan A+\tan B+\tan C} \right)\);

a₁x + b₁y + c₁ = 0

a₂x + b₂y + c₂ = 0

a₃x + b₃y + c₃ = 0

If the equation of the lines are given, then firstly determine the two altitudes of a triangle.

Equation for an AP

\(\frac{{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}}{{{a}_{1}}{{a}_{3}}+{{b}_{1}}{{b}_{3}}}=\frac{{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}}{{{a}_{2}}{{a}_{3}}+{{b}_{2}}{{b}_{3}}}\);

And for a BM

\(\frac{{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}}{{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}}=\frac{{{a}_{3}}x+{{b}_{3}}y+{{c}_{3}}}{{{a}_{2}}{{a}_{3}}+{{b}_{2}}{{b}_{3}}}\);

After solving AP and BM, we get the orthocenter.

Note:

The centroid of a triangle divides median in the ratio 2:1
For the right-angled triangle, the coordinates of vertex containing the right angle are actually the coordinates of orthocenter.
The orthocenter(O), centroid (G) and circumcenter (C), of any triangle lie in a same straight line and G divides the join of O and C in the ratio of 2:1.
The circumcenter of a right-angled triangle is the mid-point of hypotenuse.
In an equilateral orthocenter, centroid, circumcenter, incentre coincide

Example: The orthocenter of the triangle formed by (0, 0), (8, 0) and (4, 6) is

Solution: Given that O (0, 0), A (8, 0) and B (4, 6)

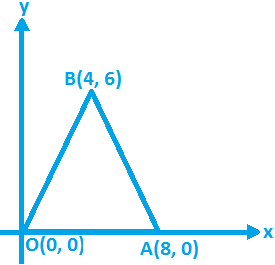
Line perpendicular to OA passing through B is x = 4

Line perpendicular to AB through origin is y = 2/3x.

The point of intersection of a line x = 4 and y = 2/3x is \(\left( 4,\frac{8}{3} \right)\).