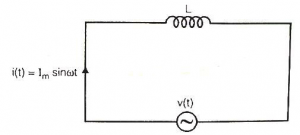
 \(V\left( t \right)=L\frac{di}{dt}\)
\(V\left( t \right)=L\frac{di}{dt}\)
V(t) = ωL Im cos ωt
V(t) = XLIm cos ωt
Where; XL = ωL; XL is known as inductance of circuit and has a unit of “ohm”
V(t) = XLIm sin (ωt + 90⁰)
And instantaneous power
p(t) = v (t) * i(t)
= Vm cos ωt Im sin ωt
\(p\left( t \right)=\frac{{{V}_{m}}{{I}_{m}}}{2}\sin 2~\omega t~\)So average power is \({{P}_{avg}}=\frac{1}{2\pi }~\underset{0}{\overset{2\pi }{\mathop \int }}\,p\left( t \right)~d\omega t=0\)
Hence in positive half cycle of the power, inductor takes energy from the source and in the negative cycle inductor delivers energy to the source. Hence not power dissipation is zero.
From above mathematical expressions we can draw phasor diagram of rms value of voltage and current.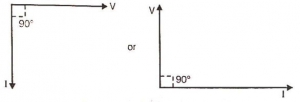 From vector diagram it is clear that in an inductor current lags to voltage by (or voltage leads to currents by 90⁰).
From vector diagram it is clear that in an inductor current lags to voltage by (or voltage leads to currents by 90⁰).
