If the particle moves in the circle with a uniform speed, we call it a uniform circular motion. In this case, dv/dt = 0 and equation gives \(\overrightarrow{\alpha }=-{{\omega }^{2}}r\overrightarrow{{{e}_{r}}}\).
Thus, the acceleration of the particle is in the direction of \(-\overrightarrow{{{e}_{r}}}\), that is, towards the centre. The magnitude of the acceleration is α = ω²r
\(=\frac{{{v}^{2}}}{{{r}^{2}}}r=\frac{{{v}^{2}}}{r}\).
Thus, if a particle moves in a circle of radius r with a constant speed v, its acceleration is v²/r directed towards the centre. This acceleration is called centripetal acceleration. Note that the speed remains constant, the direction continuously changes and hence the “velocity” changes and there is an acceleration during the motion.
\(=\frac{2\pi \times 10cm}{4s}=5\pi cm/s\).
The linear acceleration is \(\alpha =\frac{{{v}^{2}}}{r}=\frac{{{\left( 5\pi \,cm/s \right)}^{2}}}{10\,cm}=25{{\pi }^{2}}\,cm/{{s}^{2}}\).
This acceleration is directed towards the centre of the circle.
Non uniform circular motion: If the speed of the particle moving in a circle is not constant, the acceleration has both the radial and the tangential components. According to equation, the radial and the tangential acceleration are \({{\alpha }_{r}}=-{{\omega }^{2}}r=-\frac{{{v}^{2}}}{r}\) and \({{\alpha }_{t}}=\frac{dv}{dt}\).
Thus, the component of the acceleration towards the centre is ω²r = – v²/r and the component along the tangent (along the direction of motion) is dv/dt. The magnitude of the acceleration is \(\alpha =\sqrt{{{\alpha }^{2}}_{r}+{{\alpha }^{2}}_{t}}=\sqrt{{{\left( \frac{{{v}^{2}}}{r} \right)}^{2}}+{{\left( \frac{dv}{dt} \right)}^{2}}}\).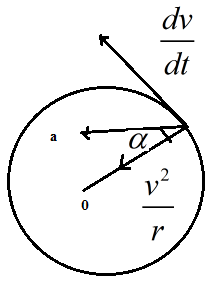
The direction of this resultant acceleration makes an angle α with the radius
where \(\tan \alpha =\frac{\left( \frac{dv}{dt} \right)}{\left( \frac{{{v}^{2}}}{r} \right)}\).