Torque on an Electric Dipole in a Uniform Electric Field

Torque on an Electric Dipole in a Uniform Electric Field

Consider a dipole with charges +q and –q forming a dipole since they are a distance d away from each other. Let it be placed in a uniform electric field of strength E such that the axis of the dipole forms an angle θ with the electric field.

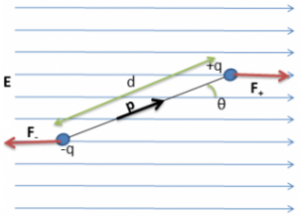
The force on the charges is

\(\overrightarrow{{{F}_{+}}}\,=\,+\,q\overrightarrow{E}\)

\({{\overrightarrow{F}}_{-}}\,=\,-\,q\overrightarrow{E}\)

The components of force perpendicular to the dipole are:

\({{F}_{+}}^{\bot }\,=\,+\,qE\,\sin \theta \)

\({{F}_{-}}^{\bot }\,=\,-\,qE\,\sin \theta \).

Since the force magnitudes are equal and are separated by a distance d, the torque on the dipole is given by:

Torque (\(\tau \)) = Force \(\times \) Distance Separating Forces

\(\tau \,=\,dqE\,\sin \theta \)

Since dipole moment is given by:

\(p\,=\,qd\)

And the direction of the dipole moment is from the positive to the negative charge, it can see from the above equation that the torque is the cross product of the dipole moment and electric field. Notice that the torque is in the clockwise direction (hence negative) in the above figure. If the direction of Electric Field is positive.

Thus,

\(\tau \,=\,-\,pE\,\sin \theta \)

Or,

\(\overrightarrow{\tau }\,=\,\overrightarrow{p}\,\times \,\overrightarrow{E}\)

\(\left| \overrightarrow{\tau } \right|\,=\,\left| \overrightarrow{p}\,\times \,\overrightarrow{E} \right|\,=\,pE\,\sin \theta \)