Tangent to the circle: Circle is a line that touches the circle at exactly one point is called tangent to the circle (or) A tangent to a curve at a point is a straight line that touches the curve at that point.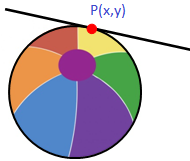
Equation of tangent: The equation of the tangent at p(x₁, y₁) of the circle
S = 0 circle
x² + y² + 2gx + 2fy + c = 0 is s₁ = 0
xx₁ + yy₁ + g (x + x₁) + f (y + y₁) + c = 0
The equation of the tangent to the circle x² + y² = r² at P(x₁, y₁) s₁ = 0.
xx₁ + yy₁ = r²
Examples of Tangent: The line AB is a tangent to the circle at P.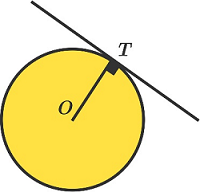
A tangent line to a circle contains exactly one point of the circle.
A tangent to a circle is at right angles to the radius of the circle at its point of contact
Normal to the circle: The normal at any point P of the center is the line which passes through P and is perpendicular to the tangent at P (or) the tangent draws the perpendicular line is called normal to the circle.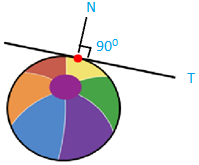
Equation of Normal: The equation of the normal at p(x₁, y₁) of the circle.
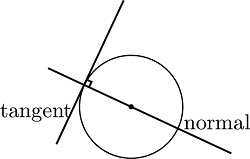S = 0.
x² + y² + 2gx + 2fy + c = 0 is (x – x₁) (y₁ + f) – (y – y₁) (x₁ + g) = 0.
The equation of the normal to the circle x² + y² = r² at p(x₁, y₁) is xy₁ – yx₁ = 0.
The line lx + my + n = 0 is a normal to the circle x² + y² + 2gx + 2fy + c = 0 if and only if gl + mf = n.