Projectile motion

Projectile motion is a form of motion in which an object or particle (called a projectile) is thrown near the earth’s surface, and it moves along a curved path under the action of gravity only.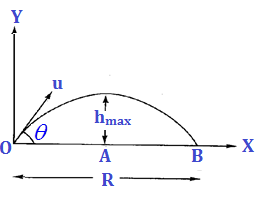Motion along Horizontal direction: A body projected from the ground with a velocity u at an angel with the horizontal.

Horizontal components of the velocity at time t is v_x = u cos θ

The horizontal distances covered in time t is x = (u cos θ) t

Motion along Vertical direction: Vertical components of the velocity at time t is v_y = u sinθ – gt

The vertical distance covered in time t is

y = (u sin θ) t – ½ gt²

Equation of trajectory: y = (tan θ) x – gx² / 2u² cos²θ

It is in the form of y = Ax + Bx², which represents a parabola (where A = tan , B = – g / 2u² cos²θ)

Resultant velocity at time t: Magnitude of resultant velocity at time t is v = (v²_x + v²_y) ^½

The angle subtended by the resultant velocity vector with the horizontal is given by tan α = v_y / v_x

Time of flight (T): We know the general equation in vertical direction is y = (u sin θ) t – ½ gt²

For time of flight y=0

0= u sin θT – ½ gT²

U sinθ = gT/2

T = 2usinθ /g

Maximum height attained: We know the general equation in vertical direction is V²_y – U²_y = 2a_ys

For maximum height 0 – u² sin²θ = 2 (-g) h_max

h_max = u² sin²θ/2g

Horizontal range: We know the general equation in vertical direction is x = u cos θt

For range t = T

R = ucosθ * 2usinθ/g

R = u² sin (2θ)/g.

Applications

⇒ The horizontal range is the same for angles θ and (90⁰ – θ).

⇒ The horizontal range is maximum for θ = 45⁰. R_max = u²/g

⇒ When horizontal range is maximum, h_max = R_max/4

⇒ At the point of projection, KE = ½ mu², PE = 0. Total energy E = ½ mu².

⇒ At the highest point, KE = ½ mu²cos²θ and PE = total energy – KE = ½ mu² – ½ mu²cos²θ = ½ mu²sin²θ

⇒ To find R and from the equation of trajectory y = ax – bx²

Where a and b are constants, refer to this figure.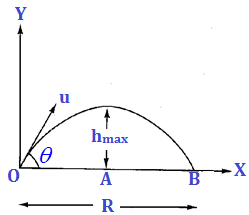a) At O and B, y = 0. Putting y = 0 in the above equation, we have 0 = ax – bx²=> x = 0, x = a/b. Therefore R = a/b

b) At A y = h_max and x = R/2 = a/2b. Using these values in y = ax – bx², we get h_max = a²/4b

⇒ If A and B are two points at the same horizontal level on a trajectory at a height h from the ground,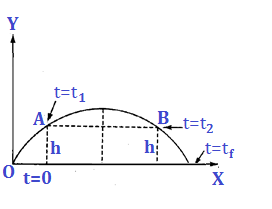a) t_f= 2usinθ/g = t₁ + t₂

b) h = ½ g t₁t₂

c) Average velocity during time interval (t₂ – t₁) is v_av = ucosθ (·.· during this interval, the vertical displacement is zero).