Polar Equation – Circle
Pole and Polar: Let S = 0 be a circle and P be a point. If any line drawn through the point P meets the circle in two points A and B then the point of intersection of the tangent drawn at A and B lie on a line called the polar of P with respect to the S = 0 and P is called the pole of the polar line.
Theorem: The equation of the polar of the point P (x, y) with respect to the circle S = 0 is S₁ = 0
Proof: Let S ≡ x² + y² + 2gx + 2fy + c = 0 be the given circle let the chord (secant line) through P meets the circle in A and B.
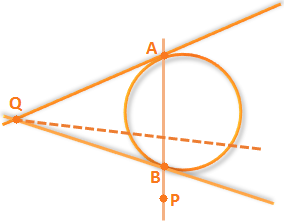
Let Q (x₂, y₂) be the point of intersection of the tangents drawn at A and B to the circle as show in figure.
Now AB is the chord of contact of Q with respect to S = 0
Therefore, the equation of AB is S₂ = 0 ⇒ xx₂ + yy₂ + g (x + x₂) + f (y + y₂) + c = 0
Since AB is passes through P, we get x₁ x₂ + y₁ y₂ + g (x₁ + x₂) + f (y₁ + y₂) + c = 0
Q lies on the line xx₁ + yy₁ + g (x + x₁) + f (y + y₁) + c = 0
Therefore, the equation of the polar of P is S₁ = 0
Notes:
⇒ If P lies outside the circle S = 0 then the polar of P meets the circle in two points and the polar becomes the chord of contact of P
⇒ If P lies on the circle S = 0 then the polar of P becomes the tangent at P to the circle S = 0
⇒ If P lies inside the circle S = 0, then the polar of P does not meet the circle.
⇒ If P is the Centre of the circle S = 0, then the polar of P with respect to S =0 does not exits
Example: Find the polar of the P (3, -1) with respect to 2x² + 2y² = 11
Solution: The equation of the circle in standard form is 2x² + 2y² = 11
2/2x² + 2/2y² = 11/2
x² + y² – 11/2 = 0
the equation of polar of (3, -1) with respect to the given circle is S₁ = 0
⇒ xx₁ + yy₁ – 11/2 = 0
⇒ 3x + y – 11/2
⇒ 6x + 2y – 11 = 0.
