Point of Contact and Tangent to the Circle

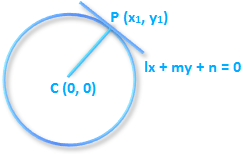
Point of Contact and Tangent to the Circle

Theorem: The condition that the straight-line lx+ my + n = 0 may touch the circle x² + y² = a² is n² = a² (l² + m²) and the point of contact is \(\left( \frac{-{{a}^{2}}l}{n},\frac{-{{a}^{2}}m}{n} \right)\).

Proof: The given line is lx + my + n = 0 … (1)

The given circle is x² + y² = r² … (2)

Center C = (0, 0)

Radius = r

Line (1) is a tangent to the circle (2)

⇔ The perpendicular distance from the center C to the line (1) is equal to the radius r.

(∵ We know that perpendicular distance from point to line \(\frac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\)).

⇔ |lx + my + n|/ √ (l² + m²) = r

⇔ |l (0) + m (0) + n|/√ (l² + m²) = r

⇔ |n|= r √ (l² + m²)

Squaring on both sides

⇔ n² = r² (l² + m²)

Let P (x₁, y₁) be the point of contact.

Equation of the tangent is S₁ = 0 ⇒ xx₁ + y y₁ – r² = 0

Equation (1) and above equation are representing the same line, therefore \(\frac{{{x}_{1}}}{l}=\frac{{{y}_{1}}}{m}=\frac{-{{a}^{2}}}{n}\).

Therefore, point of contact is \(\left( \frac{-{{a}^{2}}l}{n},\frac{-{{a}^{2}}m}{n} \right)\).

Theorem: The condition for the straight-line lx + my + n = 0 may be a tangent to the circle x² + y² + 2gx +2 f y + c = 0 is (g² + f² – c) (l² + m²) = (lg + mf – n) ²

Proof: Line lx + my + n = 0

Circle is x² + y² + 2gx +2 f y + c = 0

Center of the circle (C) is (-g, -f) and radius is r = √ (g² + f² – c)

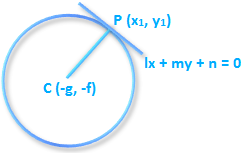
⇔ Perpendicular distance C to the line (1) is equal to the radius r.

⇔ |lx + my + n|/√ (l² + m²) = r

⇔ |l (-g) + m (-f) + n|/√ (l² + m²) = √ (g² + f² – c)

⇔ (lg + mf +n) = √ (l² + m²) √ (g² + f² – c)

Squaring on both sides

⇔ (lg + mf +n)² = (l² + m²)  (g² + f² – c).