Permutations
Number of permutations of n different thing taken all at a time is n!
Proof:
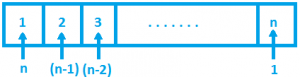
By the multiplication rule, the number of ways of filling up the first, second, third … nth places together is n (n – 1) (n – 2) …. 2 x 1 = n!.
\(^{n}{{P}_{n}}{{=}^{n}}{{P}_{n-1}}=n!\).
Factorial Zero: From the formula, we have
\(^{n}{{P}_{r}}=\frac{n!}{0!}\) … (1)
Also, the number of permutations of n different things taken all at a time in n! … (2)
From equation (1), the number of permutations of n different things taken all at a time
\(^{n}{{P}_{n}}=\frac{n!}{0!}\) … (3)
From (2) and (3), we have
\(n!=\frac{n!}{0!}\) … (4)
Again equation (4) will be valid only 0! Is taken as 1.
Thus 0! has no meaning from the definition of factorial
But in order to make the formula for \(^{n}{{P}_{r}}=\frac{n!}{(n-r)!}\) valid for r = n, 0! is taken as 1.
Meaning of 1/(-k)! where k is a positive integer:
\(^{n}{{p}_{r}}=\frac{n!}{(n-r)!}\).
Putting r = n + k, we have
\(^{n}{{p}_{n+k}}=\frac{n!}{(-k)!}\).
But, the number of ways of arranging n + k out of n different things is 0. Therefore,
\(\frac{n!}{(-k)!}=0\).
I.e., \(\frac{1}{(-k)!}=0\).
Example: If \(^{9}{{P}_{5}}+5{{\ }^{9}}{{P}_{4}}{{=}^{10}}{{P}_{r}}\), find the value of r.
Solution: Given that \(^{9}{{P}_{5}}+5{{\ }^{9}}{{P}_{4}}{{=}^{10}}{{P}_{r}}\).
\(=\frac{9!}{(9-5)!}+5\ \frac{9!}{(9-4)!}\).
\(=\frac{9!}{4!}+5\times \frac{9!}{5!}\).
\(=\frac{9!}{4!}+5\times \frac{9!}{5\times 4!}\).
\(=\frac{9!}{4!}+\frac{9!}{4!}\).
\(=2\times \frac{9!}{4!}\).
\(=2\times \frac{5\times 9!}{5\times 4!}\).
\(=\frac{10\times 9!}{5!}\).
\(=\frac{10!}{5!}\).
\(^{10}{{P}_{r}}{{=}^{10}}{{P}_{5}}\).
The value of r is 5.
