Parametric Equations of a Circle
If P (x, y) is a point on the circle with center C (h, k) and radius r, then x = h + r sin θ, y = k = r cos θ where 0 ≤ θ < 2π.
Proof: Let θ be the angle made by the line \(\overleftrightarrow{CP}\) with x – axis in the positive direction let D, M be the projections of C, P on x – axis respectively.
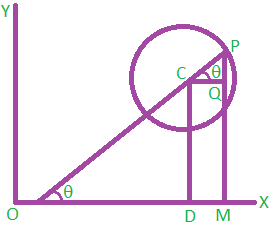
Let Q be the projection of C on PM.
Now ∠PCQ = θ
cos θ = CQ/ CP,
sin θ = PQ/ CP
Therefore CQ = CP Cosθ
= r Cosθ
PQ = CP sinθ
= r sinθ
x = OM = OD + DM
=OD + CQ
= h + r cosθ
Y = PM = PQ + QM
= PQ + CD
= k + r sinθ
A point on the circle x² + y² = r² is taken in the form (r cosθ, r sinθ). The point (r cosθ, r sinθ). is simply denoted as point θ.
Example 1: The parametric equation of the circle (x-3) ² + (y-6) ² = 8².
Solution: Given that
(x-3) ² + (y-6) ² = 8²
Above equation h = 3, k = 6 and r = 8
The parametric equations are
x = h + r cosθ
y = k + r sinθ
x = 3 + 8 cosθ
y = 6 + 8 sinθ
where 0 ≤ θ < 2π
Example 2: Find the parametric equation of the circle 4(x² + y²) = 9.
Solution: Given circle equation is 4(x² + y²) = 9
(x² + y²) = 9/4
x² + y² = (3/2)² … (1)
center (h, k) = (0, 0)
radius (r) = 3/2
the parametric equation are
x = h + r cosθ
y = k + r sinθ
x = 0 + 3/2 cosθ,
y = 0 + 3/2 sinθ. where 0 ≤ θ < 2π.
