Parabola
Theorem: Three normal can be drawn from a point (x₁, y₁) to the parabola y² = 4ax.
If the normal at t₁ and t₂ to the parabola y² = 4ax meet on the parabola, then t₁t₂ = 2.
Proof: Let the normal at t₁ and t₂ meet at t₃ on the parabola
The equation of the normal at t₁ is y + xt₁ = 2at₁ + at₁³ … (1)
Equation of the chord joining t₁ and t₃ is y (t₁ + t₃) = 2x + 2at₁t₃ … (2)
from equation (1) and (2) represent the same line
Therefore \(\frac{{{t}_{1}}+{{t}_{3}}}{1}=\frac{-2}{{{t}_{1}}}\),
\({{t}_{3}}=-{{t}_{1}}-\frac{2}{{{t}_{1}}}\),
Similarly, t₃ = -t₂ – 2/t₂
Therefore \(-{{t}_{1}}-\frac{2}{{{t}_{1}}}=-{{t}_{2}}-\frac{2}{{{t}_{2}}}\),
\({{t}_{1}}-{{t}_{2}}=\frac{2}{{{t}_{2}}}-\frac{2}{{{t}_{1}}}\),
\({{t}_{1}}-{{t}_{2}}=\frac{2({{t}_{1}}-{{t}_{2}})}{{{t}_{1}}{{t}_{2}}}\),
t₁ t₂ = 2
Example: Show that the tangent at one extremity of a focal chord of a parabola is parallel to the normal at the other extremity.
Solution: P(t₁), Q(t₂) are the ends of a focal chord
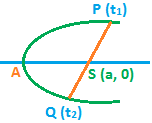
Slope of PS = Slope of PQ
\(\frac{2a{{t}_{1}}}{a({{t}_{1}}^{2}-1)}=\frac{2a({{t}_{1}}-{{t}_{2}})}{a({{t}_{1}}^{2}-{{t}_{2}}^{2})}\),
\(\frac{{{t}_{1}}}{{{t}_{1}}^{2}-1}=\frac{1}{{{t}_{1}}+{{t}_{2}}}\),
\({{t}_{1}}+{{t}_{2}}=\frac{{{t}_{1}}^{2}-1}{{{t}_{1}}}={{t}_{1}}-\frac{1}{{{t}_{1}}}\),
\({{t}_{2}}=\frac{-1}{{{t}_{1}}}\)… (1)
Equation of the tangent at P(t₁) is t₁y = x + at₂²
slope of the tangent at P = 1/t₁ … (2)
y + xt₂ = 2at₂ + at₂²
Slope of the normal at Q = -t₂ … (3)
From equation (1), (2), (3) we get
Slope of the tangent at P = slope of normal at Q.
Slope of the tangent at P is parallel to the normal at Q.
