L-R Series circuit (inductor in series with resistor):
A resistor-inductor circuit (RL circuit) is an electric circuit composed of resistors and inductors driven by a voltage or current source. A first order RL circuit is composed of one resistor and one inductor and is the simplest type of RL circuit.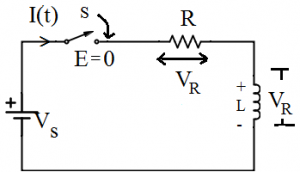
Using Kirchhoff’s voltage law
According to the law, the sum of voltages at junction is zero. The sum of the voltage due to the resistance as well as the inductance should be zero.
V(t) = VR + VL
⇒ voltage in resistor
VR = IR
⇒ voltage in inductor
⇒ \({{V}_{L}}=L\frac{di}{dt}\).
⇒ \(V(t)=IR+L\frac{di}{dt}\).
⇒ \(I(t)={{I}_{0}}\left[ 1-{{e}^{-t\tau }} \right]\).
⇒ \(I(t)=\frac{V}{R}\left[ 1-{{e}^{\frac{Rt}{L}}} \right]\).
⇒ \(\tau =\frac{L}{R}\)→ Time constant
⇒ \(I=\frac{V}{R}\)→ Steady state current
Transient curve for an LR series circuit: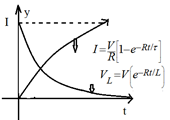
R-C CIRCUIT (Capacitor series with Resistor):
A resistor–capacitor circuit (RC circuit) is an electric circuit composed of resistors and capacitors driven by a voltage or current source. A first order RC circuit is composed of one resistor and one capacitor and is the simplest type of RC circuit.
RC circuits can be used to filter a signal by blocking certain frequencies and passing others.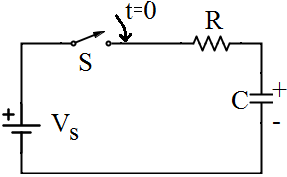
Apply Kirchoff’s voltage law
⇒ \(\frac{q}{c}=IR\).
⇒ \(\frac{q}{c}=\frac{dq}{dt}R\).
⇒ \(\frac{dq}{q}=-\int\limits_{0}^{t}{\frac{dt}{RC}}\).
⇒ q = qₒe-t/t
⇒ \(I=\frac{dq}{dt}\).
⇒ \(\frac{dq}{dt}=\frac{d\left( {{q}_{0}}{{e}^{-t/\tau }} \right)}{dt}\).
⇒ I = Iₒ e-t/t
⇒ \(I=\frac{V}{R}{{e}^{-t/\tau }}\).
t = RC is time constant for an RC circuit.
\({{I}_{0}}=\frac{V}{R}\) is maximum current in RC circuit.
In AC Circuit:
|
Type of circuit |
Impedance |
|
Purely resistive circuit |
Z = R |
| Purely inductive circuit |
Z = XL = ωL |
|
Purely capacitive circuit |
\(\[Z={{X}_{c}}=\frac{1}{{{\omega }_{c}}}\) |
|
L-R Circuit |
\(\[Z=\sqrt{{{R}^{2}}+X_{L}^{2}}\) |
| L-C circuit |
\(\[Z=\sqrt{{{R}^{2}}+X_{c}^{2}}\) |
| L-C-R circuit |
\(Z=\sqrt{{{R}^{2}}+{{\left( {{X}_{L}}-{{X}_{c}} \right)}^{2}}}\) |