LCR Circuit
We know that there are two types of connection series and parallel. Series circuit is one in which current remains the same along each element. Now we will talk about LCR circuit. The LCR circuit analysis can be understood better in terms of phasors. A phasor is a rotating quantity.
For an inductor (L), if we consider I to be our reference axis, then voltage leads by 90° and for the capacitor the voltage lags by 90°. But the resistance, current and voltage phasors are always in phase.
Analysis of an LCR Circuit – Series Circuit: Let’s consider the following LCR circuit using the current across the circuit to be our reference phasor because it remains the same for all the components in a series LCR circuit.
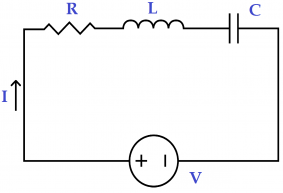
As described above the overall phasor will look like below:
From the above phasor diagram we know that,
V² = (VR)² + (VL – VC)² … (1)
Now Current will be equal in all the three as it is a series LCR circuit. Therefore,
VR = IR … (2)
VL = IXL … (3)
VC = IXC … (4)
Using equations 1, 2, 3 and 4. We get:
\(I\,=\,\frac{V}{\sqrt{{{R}^{2}}\,+\,{{\left( {{X}_{L}}\,-\,{{X}_{C}} \right)}^{2}}}}\).
Also the angle between V and I is known phase constant,
\(\tan \,\phi \,=\,\frac{{{V}_{L}}\,-\,{{V}_{C}}}{R}\).
It can also be represented in terms of impedance,
Tan φ = XL – XC R
Depending upon the values of XL and XC.
We have three possible conditions:
- If XL > XC, then tanφ > 0 and the voltage leads the current and the circuit is said to be inductive.
- If XL < XC, then tanφ < 0 and the voltage lags the current and the circuit is said to be capacitive.
- If XL = XC, then tanφ = 0 and the voltage is in phase with the current and is known as resonant circuit.
