Isentropic Process

Isentropic Process

Isentropic means constant entropy. A process during which the entropy remains constant is called an isentropic process, which is characterized by ΔS = 0 Or S₁ = S₂ for a process 1 – 2.

If a process is both reversible and adiabatic, then it is an isentropic process.

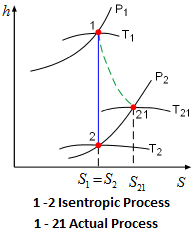
An isentropic process is an idealization of an actual process and serves as a limiting case for an actual process.

\(\operatorname{Re}versible\,\,\Rightarrow \,dS=\,{{\int\limits_{1}^{2}{\left( \frac{\delta Q}{T} \right)}}_{rev}}\)

Adiabatic ⇒ Q = 0

⇒ dS = 0

Example: Isentropic Expansion in Gas Turbine

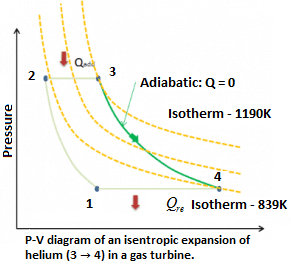
Assume an isentropic expansion of helium (3 → 4) in a gas turbine. Since helium behaves almost as an ideal gas, use the ideal gas law to calculate outlet temperature of the gas (T₄). In this turbine the high-pressure stage receives gas (point 3 at the figure: P₃ = 6.7 MPa; T₃ = 1190 K (917°C) from a heat exchanger and exhaust it to another heat exchanger, where the outlet pressure is P₄ = 2.78 MPa (point 4).

Explanation: The outlet temperature of the gas, T₄ can be calculated using P, V, T relation for isentropic process (reversible adiabatic process):

\(\frac{{{P}_{1}}}{{{P}_{2}}}\,=\,{{\left[ \frac{{{V}_{2}}}{{{V}_{1}}} \right]}^{k}}\,=\,{{\left[ \frac{{{T}_{1}}}{{{T}_{2}}} \right]}^{\frac{k}{k-1}}}\),

In this equation the factor for helium is equal to \(k\,=\,\frac{{{C}_{p}}}{{{C}_{v}}}\,=\,1.66\). From the previous equation follows that the outlet temperature of the gas, T₄ is:

\({{T}_{4}}\,=\,{{\left[ \frac{{{P}_{4}}}{{{P}_{3}}} \right]}^{\frac{k-1}{k}}}\times {{T}_{3}}\,=\,{{\left[ \frac{2.78}{6.7} \right]}^{\frac{0.66}{1.66}}}\times 1190\,=\,839K\,\).