Instantaneous velocity: It is defined as the rate of change of position for a time interval which is very small almost zero. Beside Instantaneous velocity, average velocity is a way of defining how fast a body is moving. But average velocity is only the average of the velocity of body over a given time interval, and not the exact measure of velocity of a body at an instant.
The exact measure of velocity of a body at an instant or over a very – very – very short time interval Δt is known as instantaneous velocity.
Mathematically Instantaneous velocity of an object is the limiting value of average velocity as Δt tends towards zero.
\(\underset{\Delta t\to 0}{\mathop{\lim }}\,\,\frac{\Delta x}{\Delta t}\)
And Instantaneous velocity is also the derivative of the position of the object (x) with respect to time interval (t).
Instantaneous velocity = \(\frac{dx}{dt}\)
In a graph of motion of an object drawn “x” versus “t”, Instantaneous velocity of the object is the slope of tangent line drawn at the position representing that instant.
Instantaneous velocity is a vector quantity and thus have its direction associated with it along with its magnitude.
We know that the average velocity for a given time interval is total displacement divided by total time. As this time interval approaches zero, the displacement also approaches zero. But the limit of the ratio of displacement and time is non-zero and is called the Instantaneous velocity.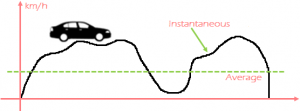 If the displacement of the particle varies with respect to time and is given as (6t² + 2t + 4) m, the Instantaneous velocity can be found out at any given time by:
If the displacement of the particle varies with respect to time and is given as (6t² + 2t + 4) m, the Instantaneous velocity can be found out at any given time by:
s = (6t² + 2t + 4)
Velocity (V) = \(\frac{ds}{dt}\)
\(=\,\frac{d(6{{t}^{2}}+2t+4)}{dt}\)
= 12 t + 2
So, If we have to find out the Instantaneous velocity at t = 5 sec, then we will put the value of t in the obtained expression of velocity.
Instantaneous velocity at t = 5 sec = (12 x 5 + 2) = 62 m/sec
Let us calculate the average velocity now for 5 seconds.
Displacement = (6 x 5² + 2 x 5 + 4) = 164 m
Average Velocity =\(\frac{164}{5}\) = 32.8 m/sec
Did the bullet have a speed at the instant this picture was taken? And how fast were you driving at a specific point or at a specific time? To answer these questions, we need to consider a new concept known as INSTANTANEOUS SPEED. Instantaneous Speed: We know that the average speed is for a given time interval is total distance travelled divided by the total time taken. As this time interval approaches zero, the distance travelled also approaches zero. But the limit of the ratio of distance and time is non-zero and is called the Instantaneous speed.
Instantaneous Speed: We know that the average speed is for a given time interval is total distance travelled divided by the total time taken. As this time interval approaches zero, the distance travelled also approaches zero. But the limit of the ratio of distance and time is non-zero and is called the Instantaneous speed.
To understand it in simple words we can also say that instantaneous speed at any given time is the magnitude of the instantaneous velocity at that time.
If distance as a function of time is known to us, we can find out the instantaneous speed at any time. Let’s understand this by means of an example.
Distance (s) = 5t³ m
Speed (V) = \(\frac{ds}{dt}\)
\(=\frac{d(5{{t}^{3}})}{dt}\)
= 15 t²
Now, we can easily find the Instantaneous speed at any given time by putting the value of t in this Obtained Expression.
Real life Applications:
1. The speedometer of a car reveals information about the Instantaneous speed of your car. It shows your speed at a particular instant in time. On the average, your car was moving with a speed of 25 miles per hour.
2. A cheetah who is running with speed of 80 miles per hour then it is his Instantaneous speed because it is shown as in per hour speed.
How to find Instantaneous Speed?
Example: The displacement of a body is given by the equation D = at². Calculate Instantaneous speed of the body at t = 2sec, If the value of acceleration is 5 m/s²?
Solution: We know that,
Ins tan taneous velocity (IS) = \(\underset{T\to t}{\mathop{\lim }}\,\frac{dX}{dT}\)
So, here X = D and hence we have
\(IS\,=\,\underset{t\to 2}{\mathop{\lim }}\,\frac{d(a\times {{t}^{2}})}{dt}\)
\(IS=\,\underset{t\to 2}{\mathop{\lim }}\,\,(2at)\)
IS = 2 x 5 x 2 = 20 m/sec
Hence, the Instantaneous speed of the body is 20 m/sec.
