A simple formula for calculating power of complex numbers in the form of cosθ and sinθ is known as de-moivre’s theorem. The De-moivre’s theorem. If n is integer (cosθ + isinθ)n = (cosnθ + isinnθ)
Cube Roots of Unity: Let us the cube roots of z is 1
Z = 3√ (1)
Z³ = 1
Z³ – 1 = 0
We can use the a³ – b³ formula
Z³ – 1 = (z – 1) (z² + z + 1)
z – 1 = 0 à z = 1
z² + z + 1 these equation factors are
z = (-1 ± √3)/2
The cube roots are 1, ω, ω²
ω = (-1 + √3)/2, ω² = (-1 – √3)/2
Properties of Cube Roots of Unity:
Property 1: Among the three cube roots of unity one of the cube roots is real and the other two are conjugate complex numbers
The three cube roots of unity are 1, (-1 + √3)/2, (-1 – √3)/2
Property II: Square of any one imaginary cube root of unity is equal to the other imaginary cube root of unity
Therefore, suppose ω² is one imaginary cube root of unity then the other would be ω
Property III: The product of the two imaginary cube roots is 1 or, the product of three cube roots of unity is 1
Cube roots of unity are 1, ω, ω². So, product of cube roots of unity = 1 ∙ ω ∙ ω² = ω³ = 1
Property IV: ω³ = 1
We know that ω is a root of the equation z³ – 1 = 0. Therefore, ω satisfies the equation z³ – 1 = 0. Consequently, ω³ – 1 = 0 or ω = 1
Property V: The sum of the three cube roots of unity is zero i.e., 1 + ω + ω² = 0
Property VI: The reciprocal of each imaginary cube roots of unity is the other.
⇒ ω = 1/ ω² and ω² = 1/ω
Hence, we conclude that the reciprocal of each imaginary cube roots of unity is the other
Property VII: If ω and ω2 are the roots of the equation z² + z + 1 = 0 then – ω and -ω² are the roots of the equation z² – z + 1 = 0
Property VIII: the cube roots of unity when represented on a complex plane lie on vertex of an equilateral triangle inscribed in a unit circle having center at origin.one vertex being on positive real axis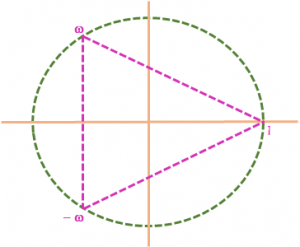
1. ω³r = 1
2. 1+ ωr + ω²r = 3 if r is multiples of 3
3. 1+ ωr + ω²r = 0 if r is not multiples 3
4. ω³r⁺¹ = ω
5. ω³r⁺² = ω²
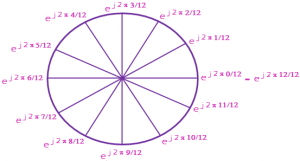
Nth Roots of Unity: if x is an nth root of unity, then it satisfies the relation xn = 1
Now, ‘1’ can also be written as cos 0 + i sin 0.
So, we have, xn = 1
= cos 0 + i sin 0
= cos 2kπ + i sin 2kπ [k is an integer]
Taking the nth root on both sides, we get
x = (cos 2kπ + i sin 2kπ)1/n
= (cos (2kπ/n) + i sin (2kπ/n)) where k = 0, 1, 2, 3, 4, …, (n – 1)
The complex numbers are in the form x + iy and are plotted on the argand or the complex plane. Also, since the roots of unity are in the form cos [(2kπ)/n] + i sin [(2kπ)/n], so comparing it with the general form of complex number, we obtain the real and imaginary parts as
Now, we see that the values of x and y satisfy the equation of unit circle with center (0, 0) i.e. x² + y² = 1.