Combination of Resistances in Series

Combination of Resistances in Series

Resistance in a conductor can be defined as the opposition offered to the flow of electrons. Resistance can be joined to each other in two ways:

1. Series Combination:

If resistances are connected in series, such that the current flowing through them is the same, the resistances are said to be in series. If I is the current flowing through the resistances, then potential drop across each is:

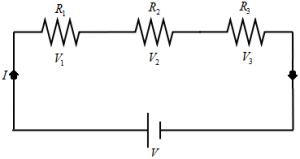
If different resistances are joined with each other such that there is only one path for the flow of electric current then the combination of such resistances is called Series Combination.

V₁ = IR₁; V₂ = IR₂; V₃ = IR₃

Adding, V₁ + V₂ + V₃ = I (R₁ + R₂ + R₃) … (1)

But, V₁ + V₂ + V₃ = V, so we get from equation (1): V = I (R₁ + R₂ + R₃)

Where V is the potential difference across the combinations, also from ohm’s law: V = IR

From equations (1) and (2), we get:

R = R₁ + R₂ + R₃

Where R = Equivalent resistance.

Characteristics:

1.In series combination Potential difference across each resistor is different depending upon the value of resistance.

2. The equivalent resistance of a circuit is equal to the sum of individual resistances.

3. In series combination current through each resistor is constant.