SECTION FORMULAE
Formula for Internal Division: The coordinates of the point which divides the line segment joining the points (x1, y1) and (x2, y2) internally in the ration m : n are given by \(x=\frac{m{{x}_{2}}+n{{x}_{1}}}{m+n}\), \(y=\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n}\).
If P is the mid-point of AB, then it divides AB in the ratio 1:1, so its coordinates are \(\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\frac{{{y}_{1}}+{{y}_{2}}}{2} \right)\).
The following diagram will help to remember the section formula.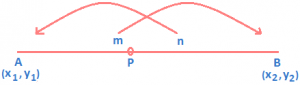
Formula for External Division: The coordinates of the points (x1, y1) and (x2, y2) externally in the ration m : n are given by \(x=\frac{m{{x}_{2}}+n{{x}_{1}}}{m+n}\), \(y=\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n}\).
Example: 1: Determine the ratio in which the line 3x + y – 9 = 0 divides the segment joining the point (1, 3) and (2, 7).
Solution: Suppose the line 3x + y – 9 = 0 divides the line segment joining A (1, 3) and B (2, 7) in the ratio k:1 at point C.
Then, the coordinates of C are \(\left( \frac{2k+1}{k+1},\,\frac{7k+3}{k+1} \right)\)
But, C lies on 3x + y – 9 = 0.
Therefore, \(3\left( \frac{2k+1}{k+1} \right)+\frac{7k+3}{k+1}-9=0\)
=> 6k + 3 + 7k + 3 – 9k – 9 = 0
=> k = ¾
So, the required ratio is 3:4 internally.
Example 2: Prove that (4, -1), (6, 0), (7, 2) and (5, 1) are the vertices of a rhombus. Is it a square?
Solution: Let the given points be A, B, C and D respectively.
Then, coordinates of the mid-points of AC are \(\left( \frac{4+7}{2},\,\frac{-1+2}{2} \right)=\left( \frac{11}{2},\,\frac{1}{2} \right)\)
Coordinates of the mid-points of BD are \(\left( \frac{6+5}{2},\,\frac{0+1}{2} \right)=\left( \frac{11}{2},\,\frac{1}{2} \right)\)
Thus, AC and BD have the same mid-point.
Hence, ABCD is a parallelogram.
Now, \(AB=\sqrt{{{\left( 6-4 \right)}^{2}}+{{\left( 0+1 \right)}^{2}}}=\sqrt{5}\),
AB = BC
So, ABCD is a parallelogram whose adjacent sides are equal.
Hence, ABCD is a rhombus.
We have, \(AC=\sqrt{{{\left( 7-4 \right)}^{2}}+{{\left( 2+1 \right)}^{2}}}=3\sqrt{2}\)
And, \(BD=\sqrt{{{\left( 6-5 \right)}^{2}}+{{\left( 0-1 \right)}^{2}}}=\sqrt{2}\)
Clearly, AC ≠ BD.
So, ABCD is not a square.
CO-ORDINATES OF CENTROID, IN-CENTRE, EX-CENTRES, ORTHOCENTRE AND CIRCUMCENTRE:
Centroid of Triangle: The coordinates of the centroid of the triangle whose vertices are (x1, y1), (x2, y2) and (x3, y3) are
\(\left( \frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\frac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)\).
Also, deduce that the medians of a triangle are concurrent.
IN-Centre of a Triangle: The coordinates of the in-center of a triangle whose vertices are
(x1, y1) , (x2, y2) and (x3,y3) are \(\left( \frac{a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}}}{a+b+c},\frac{a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}}}{a+b+c} \right)\).
EX-Centres of a Triangle: Let A (x1, y1), B (x2, y2) and C (x3, y3) be the vertices of the triangle ABC
And let a, b, c be the lengths of the sides BC, CA, AB respectively.
The coordinates of I1 are given by \(\left( \frac{-a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}}}{-a+b+c},\frac{-a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}}}{-a+b+c} \right)\)
The coordinates of I2 and I3 (centers of described circles opposite to the angles B and C respectively) are given by \({{I}_{2}}\left( \frac{a{{x}_{1}}-b{{x}_{2}}+c{{x}_{3}}}{a-b+c},\frac{a{{y}_{1}}-b{{y}_{2}}+c{{y}_{3}}}{a-b+c} \right)\) and \({{I}_{3}}\left( \frac{a{{x}_{1}}+b{{x}_{2}}-c{{x}_{3}}}{a+b-c},\frac{a{{y}_{1}}+b{{y}_{2}}-c{{y}_{3}}}{a+b-c} \right)\) respectively.
ORTHOCENTRE: If A (x1, y1) (x2, y2) and C (x3, y3) are the vertices of a triangle ABC. Then the point of intersection of intersection of its altitudes is known as the orthocenter and the coordinates are \(\left( \frac{{{x}_{1}}\tan A+{{x}_{2}}\tan B+{{x}_{3}}\tan C}{\tan A+\tan B+\tan C},\frac{{{y}_{1}}\tan A+{{y}_{2}}\tan B+{{y}_{3}}\tan C}{\tan A+\tan B+\tan C} \right)\)
CIRCITMCENTRE: If A (x1, y1), B (x2, y2) and C (x3, y3) are the vertices of a triangle ABC. Then the point of intersection of perpendicular bisectors of its sides is the circumcentre and its coordinates are \(\left( \frac{{{x}_{1}}\sin 2A+{{x}_{2}}\sin 2B+{{x}_{3}}\sin 2C}{\sin 2A+\sin 2B+\sin 2C},\frac{{{y}_{1}}\sin 2A+{{y}_{2}}\sin 2B+{{y}_{3}}\sin 2C}{\sin 2A+\sin 2B+\sin 2C} \right)\)
REMARK: The circumcentre O, centroid G and orthocenter O’ of a triangle are collinear and G divides O’ O in the ratio 2:1.
Example: If α, β, ɣ are the roots of the equation x3 – 3px2 + 3qx – 1 = 0, find the centroid of the triangle whose vertices are A (α, 1/α), B (β, 1/β) and C (ɣ, 1/ɣ).
SOLUTION: Since α, β, ɣ are the roots of the equation x3 – 3px2 + 3qx – 1 = 0
Therefore, α + β + ɣ = 3p, αβ + βɣ + ɣα = 3q
And, αβɣ = 1 … (i)
Let G(x, y) be the centroid of ΔABC. Then,
\(x=\frac{\alpha +\beta +\gamma }{3}\) and \(y=\frac{1}{3}\left( \frac{1}{\alpha }+\frac{1}{\beta }+\frac{1}{\gamma } \right)\)
=> \(x=\frac{\alpha +\beta +\gamma }{3}\) and \(y=\frac{\alpha \beta +\beta \gamma +\gamma \alpha }{3\alpha \beta \gamma }\)
=> \(x=\frac{3p}{3}\) and \(y=\frac{3q}{3}\) [Using (i)]
=> x = p and y = q
Hence, the coordinates of G are (p, q).