Domain & Range of a Real Function
Domain: Generally real functions in calculus are described by some formula and their domains are not explicitly stated. In such cases to find the domain of a function f (say) we use the fact that the domain is the set of all real numbers x for which f (x) is a real number.
Range: As discussed, the range of a function f (x) is the set of values of f (x) which it attains at points in its domain. For a real function the co-domain is always a subset of R. So, range of a real function f is the set of all points y such that y = f (x) where x ϵ Dom f (x).
Algorithm:
Step 1: Put f (x) = y
Step 2: Solve the equations in step 1 for x to obtain x = φ (y).
Step 3: Find the values of y for which the values of x obtained from x = φ (y) are in the domain of f.
Step 4: The set of values of y obtained in step 3 is the range of f.
Example: Find the domain and range of the function \(f\left( x \right)=\frac{1}{2-\cos 3x}\).
Solution: We have, \(f\left( x \right)=\frac{1}{2-\cos 3x}\).
Domain: We have,
-1 ≤ cos 3x ≤ 1 ” x ϵ R,
-1 ≤ – cos 3x ≤ 1
-1 ≤ 2 – cos 3x ≤ 3 ” x ϵ R
f (x) is defined for all x ϵ R.
So, domain (f) = R.
Range: Let f (x) = y. Then \(\frac{1}{2-\cos 3x}=y\)
2 – cos 3x = 1/y
cos 3x = 2 – 1/y
-1 ≤ 2 – 1/y ≤ 1 [∴ -1 ≤ cos 3x ≤ 1]
-3 ≤ -1/y ≤ -1
3 ≥ 1/y ≥ 1
⅓ ≤ y ≤ 1
y ϵ [⅓, 1]
So, range of f = [⅓, 1].
Some Standard Real Functions:
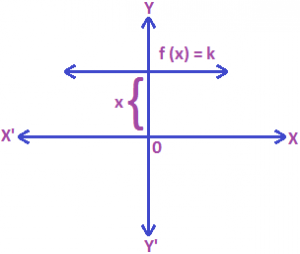
Constant Function: Let k be a fixed real number. Then a function f (x) given by f (x) = k for all x ϵ R is called a constant function. Sometimes we also call it the constant function k.
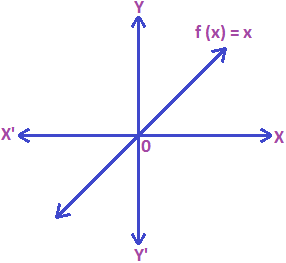
Identity Function: The function defined by I (x) = x ” x ϵ R, is called the identity function on R.
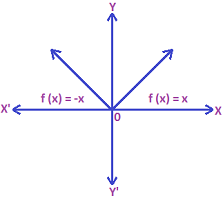
Modulus Function: The function defined by \(f\left( x \right)=\left| x \right|=\left\{ \begin{align} & x,\,\,\,when\,\,\,x\ge 0 \\ & -x,\,\,when\,\,\,x<0 \\\end{align} \right.\) is called the modulus function.
Properties of Modulus Function: The modulus function has the following properties:
i) For any real number x we have √x² = |x|.
ii) If a, b are positive real numbers then
x² ≤ a² ⇔ |x| ≤ a ⇔ – a ≤ x ≤ a.
x² < a² ⇔ |x| < a ⇔ – a < x < a
x² ≥ a² ⇔ |x| ≥ a ⇔ x ≤ – a or x ≥ a
x² > a² ⇔ |x| > a ⇔ x < – a or x > a
a² ≤ x² ≤ b² ⇔ a ≤ |x| ≤ b ⇔ x ϵ [-b, -a] È [a, b]
a² < x² < b² ⇔ a < |x| < b ⇔ x ϵ [-b, -a] È [a, b]
iii) |x + y| = |x| + |y|
(x ≥ 0 and y ≥ 0) or (x < 0 and y < 0)
iv) |x – y| = |x| – |y|
(x ≥ 0 and |x| ≥ |y| or (x ≤ 0, y ≤ 0 and |x| ≥ |y|))
v) |x ± y| ≤ |x| + |y|
vi) |x ± y| ≥ |x| – |y|
