1. The time period of a simple pendulum is
T = 2π √ (l/g)
=> T α √l or T α 1/√g
T α √ (l/g)
Using these relations. We may conclude
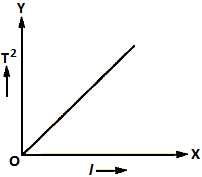
=> The graph between T2 and l is a straight line.
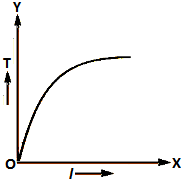
=> The graph between T and l is a parabola.
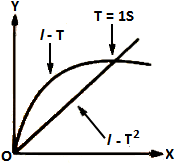
=> The graphs l – T and l – T2 intersect at T = 1s
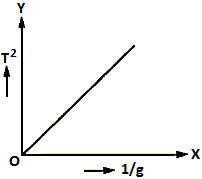
=> The graph between T2 and 1/g is a straight line.
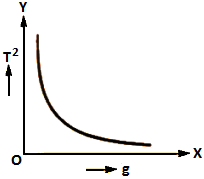
=> The graph between T2 and g is a rectangular hyperbola.
=> Finally, the graph between T and √(l/g) is also a straight line.
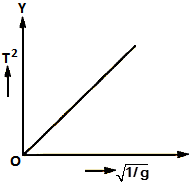
2. In the case of water oscillating in a U-tube
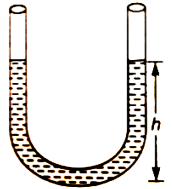
T = 2p√(l/g)
Where, h is the height of liquid column in each limb.
When a ball of mass m is made to oscillate in the nech of an air chamber having volume V and neck area A, then
T=2π\(\sqrt{\left( \frac{mV}{p{{A}^{2}}} \right)}\)
3. When a pendulum is kept in a car which is sliding down, then
T=2π\(\sqrt{\left( \frac{l}{g\cos \theta } \right)}\)
Where, θ is the angle of inclination
4. If a simple pendulum oscillates in a non-viscous liquid of density ρ, then its time period is T = 2p\(\sqrt{\left[ \frac{l}{\left( 1-\frac{s}{r} \right)g} \right]} \)
ρ = density of suspended mass.
5. If the mass m attached to a spring oscillates in a non-viscous liquid of density σ, then its time period is
T = 2π\({{\left[ \frac{m}{k}\left( 1-\frac{\sigma }{\rho } \right) \right]}^{{}^{1}/{}_{2}}}\)
Where, k = force constant.
6. If a small ball is rolling down in hemispherical bowl. Time period,
T = 2π \(\sqrt{\frac{R-r}{g}}\)
Where, R = radius of the bowl and
r = radius of the ball
7. For a body executing SHM in a tunnel dug along any chord of earth.
Time period, T = 2π\(\sqrt{\frac{{{R}_{e}}}{g}}\) = 84.6 min
Where Re is the radius of earth.
8. If the time period of simple pendulum is 2s, then it is called as second’s pendulum
9. If the simple pendulum is placed in some non-inertial frame of reference like an accelerated lift, g is replaced by geff whose value can be computed by considering the inertial force. In these cases the equilibrium position may also change.
10. If the length of simple pendulum is very large, then g can’t be taken along vertical direction.
In this case, T= 2π\(\sqrt{\frac{1}{g\left( \frac{1}{l}+\frac{1}{R} \right)}}\)
Where, R = Radius of length of the pendulum.
11. If temperature of system changes, then time period of simple pendulum changes due to change in length of the simple pendulum.
12. If a simple pendulum is in a carriage which is accelerating with an acceleration a, then
geff = g – a
eg, if the acceleration a is upwards, then
|geff|= g + a and T = 2π\(\sqrt{\frac{1}{g+a}}\)
If the acceleration a is downwards, then (g > a)
|geff|= g + a and T = 2π\(\sqrt{\frac{1}{g+a}}\)
If the acceleration a is in the horizontal direction, then
|geff|= √ (a² + g²)
In a freely falling lift, geff = 0 and T = ∞ i.e., the pendulum will not oscillate.
13. If in addition to gravity one additional force F (e.g., electrostatic force Fe) is also acting on the both, then in that case
geff = g + F/m
Here, m is the mass of the bob.
Torsional Pendulum: in a torsional pendulum, an object is suspended from a wire. If such a wire is twisted due to elasticity, it exerts a restoring torque τ = Cθ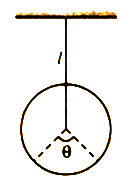 In this case, time period is given by
In this case, time period is given by
T=2π \(\sqrt{\frac{l}{C}}\)
Where, l = moment of inertia of the object
C = torsional constant of wire = \(\frac{\pi \eta {{r}^{n}}}{2l}\)
η = modulus of elasticity of wire
r = radius of wire
l = length of wire
